Important Terms and Notation

For the purposes of this post, it is important to understand a few basic notation and terms. We define further linear algebra terms in Part 1 . We will denote a vector using the following notation: \(\vec{a}\), as opposed to a scalar, \(a\). A matrix will be denoted as capital letters, \(A\). We denote random sampling via \({\stackrel{\$}{\gets}}\); for example, sampling a vector from the integers modulo \(q\) randomly is denoted: \(\vec{a} {\stackrel{\$}{\gets}}{\mathbb{Z}_q}^n\).

The output from an algorithm is defined by the following: \(F(a) \rightarrow {x}\), where \(a\) is the input itself and \(x\) is the type of the output from the function. For example, \(Square(a) \rightarrow {\mathbb{Z}}\), when \(a \in {\mathbb{Z}} \).

We refer to Learning with Errors as LWE, and Ring Learning with Errors as Ring-LWE.

Simple LWE-Based Key Exchange

Introduction and Background

Ding et al., 2012 present a “Diffie-Hellman like” key exchange protocol, in which the security of the protocol is either based on the hardness of LWE or Ring-LWE (both variations are discussed below). For the remainder of this post, we will refer to Ding et al., 2012 as DING2012. Previously in the literature, Peikert introduced a LWE-based key exchange (Peikert 2009). However, DING2012 is an improvement by making the key exchange contributory by both parties. Ding2012 also introduces the concept of Reconciliation, a mechanism which allows two parties who hold approximate agreement about a secret (in this case, the secret is a point in the lattice) to come to exact agreement (both parties are able to agree on the same lattice point, without leaking this secret lattice point to a network observer).

We will examine the protocol described in DING2012 as a simple example of a lattice-based key exchange protocol based on the hardness of LWE, in the interest of having a “starting point” to understand how more recent lattice-based key-exchange protocols are structured.

Following work such as NewHope (Alkim et al. 2016) and Frodo (Bos et al. 2016) have improved upon DING2012 while retaining a similar protocol structure, such as by making the Reconciliation algorithm more efficient or using improved sampling or encoding mechanisms. We will take a quick look at some of these below.

Key Exchange Protocol based on LWE

The below key exchange is a two-party protocol, where both parties exchange public keys over an untrusted network partition. At the end of the protocol, both parties arrive at the same shared secret. In this case, the shared secret is a point in the lattice generated by a common basis matrix \(M\) agreed upon by both parties. DING2012 presents \(M\) as a global parameter, but \(M\) can also be sent by the protocol initiator at the beginning of the exchange.

The protocol presented in DING2012 is “Diffie-Hellman like” as either party can initiate the protocol. More importantly, this protocol is contributary, meaning that both parties contribute key material that is used to derive the shared secret.

As an aside, one example of a non-contributory key exchange is a simple Key Encapsulation Mechanism (KEM), where only one party generates and sends secret key material to the other party. For example, a non-contributory KEM can be constructed by Alice first selecting a symmetric key directly, encrypting the symmetric key with Bob’s public key, and then sending the encrypted material to Bob, who decrypts the key material using his private key, thus establishing their shared secret.

We will first examine the DING2012 protocol at a high level, treating any new algorithms as a black box in order to first understand how the overall scheme is constructed. We will then dive into the Reconciliation and Hint algorithms in detail to understand why these algorithms are necessary and how they work.

Notation used in DING2012

DING2012 occasionally deviates from common notation used in lattice-based cryptography. We’ll now highlight some notation used in DING2012 that is important for the remainder of this post.

Let \(M \leftarrow {\mathbb{Z}_q}^{n \ x \ n}\) be a global parameter both parties agree on at the beginning of the protocol. This can be compared to the definition of LWE, where the lattice is generated by a basis matrix sampled uniformly at random. In the case of DING2012, this basis is denoted as \(\textbf{M}\). In practice, \(M\) can be generated by the protocol initiator and sent in the first message of the protocol.

Let \(D\) denote a discrete Gaussian distribution centered at zero. \(D\) is bounded by a standard deviation \(\sigma\).

Key Exchange

Initialization Parameters

Before beginning the key-exchange protocol, the following public parameters must be determined or generated:

- Determine \(q \in \mathbb{Z}, q \geq 2\) and \(q\) is a prime. \(q\) is used as the modulus.

- Determine \(n\), which determines the rank (meaning the length and width are equal) of the generating basis \(M\)

- Determine \(\alpha \in (0, 1)\) and \(q \geq 2\) as the parameters defining the discrete Gaussian distribution \(D\). Both secret material and error terms are sampled from \(\mathcal{D}_{\mathbb{Z}^n, \alpha q}\). However, error terms can also be sample from \(\mathcal{D}_{\mathbb{Z}, \alpha q}\), as demonstrated in Figure 1.

- Sample a uniformly random matrix \(M \leftarrow {\mathbb{Z}_q}^{n \ x \ n}\)

After generating initialization parameters, the two-party key exchange can be performed. The complete LWE-based key exchange protocol as presented in DING2012 is described in Figure 1.

The above shows that Alice’s secret is approximately equal to Bob’s shared secret, where these terms differ only by the errors added by both sides. We can see in the algorithm that once Alice and Bob both have this “approximate” secret, they can then use the Robust Extractor algorithm– denoted as RobustExtract– in Figure 1) along with the hint value \(\sigma\). By running RobustExtract with their respective approximate secret and the hint value \(\sigma\), Alice and Bob can arrive at exact agreement on a shared secret key.

We will more detail in the next section on the RobustExtract algorithm, and how to calculate the hint \(\sigma\)!

The correctness of the DING2012 key schange protocol can be concluded as follows:

\(|2({s_A}^Te_B + e_A' - {e_A}^Ts_B - e_B')| \leq 8 \cdot (\alpha q \sqrt{n}) = 8(\alpha q)^2 \cdot n \leq \frac{q}{4} - 2\)

- As demonstrated in the above equation, with overwhelming probability, if \(8(\alpha q)^2 \cdot n \leq \frac{q}{4} - 2\) (based on the bound of the norm of the Gaussian distribution):

- Because the RobustExtract algorithm has an error tolerance \( \frac{q}{4} - 2\), we can conclude \(SK_A = SK_B\).

Intuitively, the above proof says that if the bound of the errors that are sampled when performing LWE operations is less than the supported error tolerance of the RobustExtract algorithm, then both Alice and Bob’s approximate values can be safely rounded to the same exact value using the RobustExtractor.

Reconciliation

In the key exchange defined by DING2012 and referenced in Figure 1, both parties perform LWE operations and exchange public keys, which are combined to generate a single secret key. However, as both parties add errors to their public keys, as is required by the LWE problem which this protocol is based on, this entails that at the end of the key exchange, both parties will have close but not approximate shared secrets. To allow for both parties to arrive at an exact shared secret, DING2012 introduces the concepts of Reconciliation.

Reconciliation is a broader concept. To implement Reconciliation for an LWE-based protocol, we require two separate algorithms, a Hint algorithm and a Robust Extractor algorithm.

Note that DING2012 proposes a mechanism to extract a single bit from an element in \(\mathbb{Z}_q\) (in this case, a coefficient in a vector representing a lattice point). To derive the entire secret, this Reconciliation technique would need to be applied to each coefficinet in the vector.

Deriving the Hint value

The input into the Hint algorithm is one party’s “approximate secret” which is an element in \(\mathbb{Z}_q\). The output is a single bit, \(\sigma \in {0, 1}\). The purpose of the Hint Algorithm is to output a signal to be later used by the RobustExtractor algorithm to determine if one party’s “approximate” shared secret lies within a certain range or not.

The hint algorithm described by DING2012 is as follows, where the parameter \(x \in \mathbb{Z_q}\) is an “approximate” secret from one of the parties, as described in Figure 1.

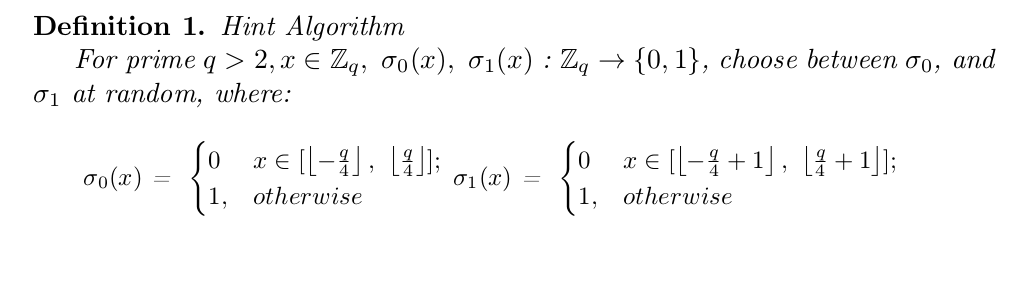
In Definition 1 of the Hint Algorithm, the requirement between randomly choosing between \(\sigma_0, \sigma_1\) is due to an observation made by Peikert in (Peikert 2014), as the Hint algorithm is otherwise biased. Randomly choosing one of the two definitions fixes the bias inherent to both definitions, if the input \(x \in \mathbb{Z}_q\) is sampled uniformly at random.

Intuitively, the Hint algorithm does the following: it takes one of the party’s "approximate" secrets, and outputs a single bit to indicate which quadrant of \(\mathbb{Z}_q\) the approximate secret falls (imagining \(\mathbb{Z}_q\) as a unit circle, divided into four quadrants). This hint will be used by both parties to determine how to round their approximate secrets, so that both parties can round to the exact value.

Extracting an Exact Secret from “Close” Values

Once one party has calculated the hint value for their approximate secret, both parties will use the same hint value along with their own "approximate" shared secret as input into the RobustExtract algorithm, where the output of performing this operation results in the exact shared secret for both parties.

Overall, the reason Bob's hint value is transmitted to Alice along with Bob's public key is because error terms are randomly sampled by both parties, and there is a chance both parties could round to different values. The hint value \(\sigma\) ensures that both parties round to the same value by transmitting a small amount of information to inform both parties about how to round their approximate shared secrets. However, transmitting \(\sigma\) over an untrusted network does not leak any useful information to a network observer, so long as the approximate secret is uniformly random.

The RobustExtract algorithm removes error terms introduced by both parties by rounding to a single point in the lattice. The hardness to an adversary to perform this same operation-- knowing only publicly-exposed information-- reduces to the hardness of LWE. Removing error terms allows both parties to arrive at the same lattice point, which is the secret value. However, knowing only public values, an adversary would need to solve LWE to similarly arrive at the same secret lattice point.

The RobustExtract algorithm is defined as follows:

The intuition behind the above definition can be a bit hard to grok, so here is an example (feel free to work through the math yourself):

- Consider the example where q=31, Alice’s secret value is 7 and Bob’s secret value is 9

- Without considering the other party’s hint value, and performing RobustExtract using their own hint value calculated for their own secret value along with their approximate shared secret, Alice will round to 1 and Bob will round 0.

- However, if Alice and Bob use the same hint value as input into the RobustExtractor with their own secret value (either Alice can send Bob her hint, or vice versa), they can arrive at the same secret value.

At a more technical level, you might observe that for the correctness of the above definition to hold, Ding2012 must require the following for the RobustExtract algorithm: First, \(|x-y|\) must be even, where \(x, y\) are the “approximate” secrets from both parties in the Key Exchange defined in Figure 1. Second, \(x-y \leq \delta\), where \(\delta\) is the error tolerance of the RobustExtractor algorithm.

The important point to take aware here is that RobustExtract extracts a single bit from a value \(x \in \mathbb{Z_q}\), by removing randomly-selected errors added by both parties and extracting the lowest bit of the input term. By using the hint value \(\sigma\) as a parity check, both parties can round to the exact value. Of course, to expand this to a multi-bit secret, RobustExtract must be used with every coefficient in the approximate secret, and so extracts a single bit from each coefficient.

DING2012: Key Exchange based on Ring-LWE

Ding2012 also defines a similar key-exchange protocol in the Ring-LWE setting. Group elements are merely defined over a ring \(R=\mathbb{Z}[x]/f(x)\), where \(f(x)=x^n+1\) and \(n\) is a power of 2, as is commonly used in Ring-LWE.

Therefore, every element is represented as an element in \(R\). For example, Alice and Bob’s secrets can be represented as \(K_A, K_B \in \mathbb{Z}[x]/f(x)\), respectively.

The correctness of the DING2012 scheme in the Ring-LWE setting relies on commutativity of ring elements. Below we can see the “approximate shared secrets” that Alice and Bob use respectively, as input into RobustExtract. Notably, these values differ only by the error terms:

\(K_A = (s_A \cdot ms_B) + 2(s_Ae_B + e_A') \)

\(K_B = (ms_A \cdot s_B) + 2(e_As_B + e_B')\)

Improved Key Exchanges, Current Work

While DING2012 is useful to understand as a simple introduction to lattice-based key exchanges, improved protocols have been presented. We will discuss a few that use similar concepts to DING2012 such as relying on Reconciliation, but highlight where these schemes have made improvements.

BCNS (Bos et al. 2015) presented a concrete instantiation of the Ring-LWE based key exchange protocol in DING2012, along with Peikert’s tweaks, such as improving the reconciliation operation (Peikert 2014). NewHope (Alkim et al. 2016) presents several improvements to the protocols presented and implemented by the BCNS authors. For example, NewHope presents improvements to the selection of the probability distribution used for sampling secret key material and error error terms to address practical requirements such as performance and resistence against timing attacks. Furthermore, NewHope presents more efficient encoding techniques for encoding bits into coefficeints, thereby improving the bandwidth efficiency of the protocol.

Frodo (Bos et al. 2016) is proposed as a key exchange protocols whose hardness relies on LWE and generic lattices alone, which is important as Ring-LWE constructed from ideal lattices does not have as long of a history of cryptanalysis as LWE and generic lattices. Frodo presents improved efficiency mechanisms, such as presenting several options to use for the LWE error distribution parameter \(\chi\). Each option is an instantiation of inversion sampling, which provides a pre-computed lookup table whose outputs are generated from a cumulative density function over a small discrete interval. Furthermore, Frodo uses a generalization of Peikert’s reconciliation mechanism (Peikert 2014) but allows for the extraction of multiple bits from a single coefficient in \(\mathbb{Z}_q\). As with NewHope, the benefit of this approach is improved efficiency and reduction of required bandwidth for the protocol, as more information can be encoded into each coefficient.

Conclusion

This has been a very short introduction to early key-exchange protocols based on the hardness of LWE and Ring-LWE. See below citations for more information, and watch the NIST Post-Quantum Competition for future standardization of post-quantum key exchanges.

Finally, if you are interested in hearing more about modern cryptography and privacy topics, you might consider following me on Twitter!